Rumus Pembulatan ke Atas: Panduan Praktis untuk Menghitung Nilai Bulat

Dalam kehidupan sehari-hari, kita sering dihadapkan dengan angka-angka yang perlu dibulatkan. Rumus pembulatan ke atas menjadi alat penting untuk memperoleh nilai bulat terdekat yang lebih besar. Di artikel ini, kita akan mengulas secara mendalam tentang rumus pembulatan ke atas, mulai dari konsep dasarnya hingga aplikasinya dalam berbagai bidang.

Pengertian Pembulatan ke Atas

Pembulatan ke atas adalah teknik matematika yang membulatkan angka ke bilangan bulat terdekat yang lebih besar.

Rumus pembulatan ke atas, yakni membagi bilangan dengan angka yang diinginkan, kemudian menaikkan hasil bagi ke bilangan bulat terdekat yang lebih besar, sangat berguna dalam berbagai bidang. Contohnya, dalam acara galaxy unpacked 2023 , kita membulatkan harga perangkat ke puluhan ribu terdekat untuk mempermudah perhitungan.

Kembali ke rumus pembulatan ke atas, jika kita membagi 17 dengan 5, hasilnya adalah 3,4. Setelah dibulatkan ke atas, hasilnya menjadi 4, yang merupakan bilangan bulat terdekat yang lebih besar dari 3,4.

Tujuannya adalah untuk menyederhanakan perhitungan dan memperkirakan nilai, terutama ketika akurasi yang tepat tidak diperlukan.

Contoh Pembulatan ke Atas

Misalnya, jika kita ingin membulatkan 3,5 ke atas, kita akan mendapatkan 4 karena 4 adalah bilangan bulat terdekat yang lebih besar dari 3,5.

Manfaat Pembulatan ke Atas

• Menyederhanakan perhitungan
• Membuat estimasi yang lebih cepat dan mudah
• Membantu menghemat waktu dan usaha

Aturan Pembulatan ke Atas

Aturan umum untuk pembulatan ke atas adalah:

• Jika angka setelah angka terakhir yang akan dibulatkan lebih besar atau sama dengan 5, angka tersebut dibulatkan ke atas.
• Jika angka setelah angka terakhir yang akan dibulatkan kurang dari 5, angka tersebut dibiarkan tidak berubah.

Rumus Pembulatan ke Atas

Pembulatan ke atas adalah teknik membulatkan angka ke bilangan bulat terdekat yang lebih besar. Rumus yang digunakan untuk pembulatan ke atas adalah:

angka_bulat = ceiling(angka)

Di mana:

• angka_bulatadalah angka bulat yang dihasilkan
• angkaadalah angka yang akan dibulatkan
• ceilingadalah fungsi pembulatan ke atas

Contoh Penerapan Rumus

Mari kita lihat beberapa contoh penerapan rumus pembulatan ke atas:

• ceiling(3,14) = 4
• ceiling(2,71) = 3
• ceiling(-1,5) =-1

Kasus Khusus

Dalam beberapa kasus khusus, rumus pembulatan ke atas perlu disesuaikan. Salah satu kasus khusus tersebut adalah ketika angka yang akan dibulatkan adalah negatif. Dalam kasus ini, rumus yang digunakan adalah:

angka_bulat = floor(angka)

1

Di mana:

• angka_bulatadalah angka bulat yang dihasilkan
• angkaadalah angka yang akan dibulatkan
• flooradalah fungsi pembulatan ke bawah

Contoh penerapan rumus pembulatan ke atas untuk kasus khusus:

• floor(-3,14) =-4
• floor(-2,71) =-3
• floor(-1,5) =-2

Cara Membulatkan ke Atas

Membulatkan ke atas adalah teknik matematika yang digunakan untuk memperkirakan angka ke nilai terdekat yang lebih besar. Proses ini sangat berguna dalam berbagai aplikasi kehidupan sehari-hari, mulai dari menghitung uang hingga mengonversi satuan pengukuran.

Langkah-langkah Membulatkan ke Atas

• Tentukan tempat desimal yang akan dibulatkan.
• Lihat angka pada tempat desimal berikutnya.
• Jika angka tersebut 5 atau lebih, tambahkan 1 ke angka pada tempat desimal yang dibulatkan.
• Jika angka tersebut kurang dari 5, biarkan angka pada tempat desimal yang dibulatkan tetap.

Contoh

Mari kita bulatkan angka 3,1415 ke atas ke tempat desimal terdekat:

• Tempat desimal yang akan dibulatkan: tempat desimal pertama
• Angka pada tempat desimal berikutnya: 4
• Karena 4 kurang dari 5, angka pada tempat desimal pertama tetap 1.

Jadi, 3,1415 dibulatkan ke atas ke tempat desimal pertama menjadi 3,2.

Aplikasi Pembulatan ke Atas: Rumus Pembulatan Ke Atas

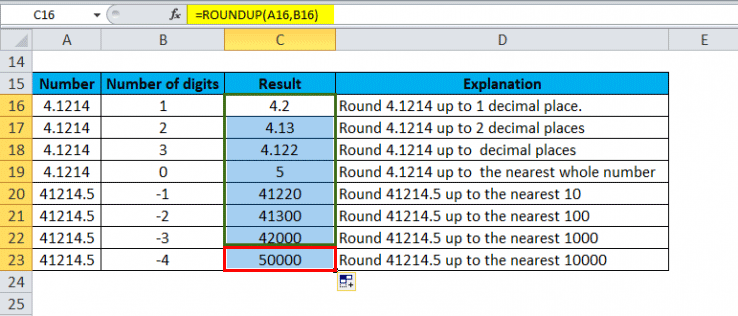
Pembulatan ke atas adalah teknik matematika yang digunakan dalam berbagai bidang kehidupan. Ini melibatkan pembulatan angka ke bilangan bulat terdekat yang lebih besar.

Identifikasi Area Umum Pembulatan ke Atas

Pembulatan ke atas banyak digunakan dalam:

• Keuangan (pembulatan harga ke atas)
• Pengukuran (pembulatan panjang ke atas)
• Pendidikan (pembulatan nilai ke atas)
• Kehidupan sehari-hari (pembulatan waktu ke atas)

Implikasi Pembulatan ke Atas

Pembulatan ke atas memiliki implikasi signifikan dalam kehidupan nyata:

• Harga yang Lebih Tinggi:Pembulatan harga ke atas dapat menyebabkan konsumen membayar lebih.
• Hasil yang Lebih Baik:Pembulatan nilai ke atas dapat meningkatkan nilai rata-rata.
• Waktu yang Lebih Efisien:Pembulatan waktu ke atas dapat menyederhanakan penjadwalan.

Contoh Spesifik

Contoh spesifik bagaimana pembulatan ke atas memengaruhi pengambilan keputusan meliputi:

• Harga Produk:Perusahaan dapat menggunakan pembulatan ke atas untuk menetapkan harga yang lebih tinggi.
• Nilai Ujian:Guru dapat menggunakan pembulatan ke atas untuk memberikan nilai yang lebih tinggi kepada siswa.
• Jadwal Bus:Jadwal bus dapat dibulatkan ke atas untuk menyederhanakan waktu keberangkatan.

Variasi Pembulatan ke Atas

Selain pembulatan ke atas standar, terdapat variasi lain yang dapat digunakan tergantung pada kebutuhan spesifik.

Pembulatan ke Atas Terdekat

Variasi ini membulatkan angka ke bilangan bulat terdekat yang lebih besar. Misalnya, 4,5 dibulatkan ke 5, dan 4,4 dibulatkan ke 4.

Pembulatan ke Atas ke Kelipatan Tertentu, Rumus pembulatan ke atas

Variasi ini membulatkan angka ke kelipatan tertentu dari angka yang ditentukan. Misalnya, membulatkan 23 ke kelipatan 5 akan menghasilkan 25, dan membulatkan 17 ke kelipatan 10 akan menghasilkan 20.

Pemilihan Variasi

Pilihan variasi pembulatan ke atas yang digunakan bergantung pada konteks dan kebutuhan aplikasi tertentu. Pembulatan ke atas standar biasanya digunakan ketika akurasi tingkat tinggi tidak diperlukan. Pembulatan ke atas terdekat dapat digunakan ketika diperlukan pembulatan yang lebih konservatif, dan pembulatan ke atas ke kelipatan tertentu dapat digunakan ketika diperlukan konsistensi atau kesederhanaan perhitungan.

Penutupan Akhir

Memahami rumus pembulatan ke atas sangat penting untuk berbagai profesi dan kegiatan sehari-hari. Dengan menerapkan rumus ini dengan benar, kita dapat memperoleh nilai bulat yang akurat dan sesuai dengan kebutuhan kita. Jadi, kuasai rumus pembulatan ke atas dan manfaatkan kekuatannya untuk mempermudah perhitungan dan pengambilan keputusan yang tepat.