Gambar topologi tree – Dalam dunia komputasi, struktur data pohon topologi memainkan peran penting dalam mengatur dan mengelola data. Gambar topologi pohon yang unik memberikan representasi visual yang jelas tentang struktur ini, membantu kita memahami cara kerjanya.
Pohon topologi, seperti namanya, menyerupai pohon dengan cabang dan daun yang terhubung ke satu titik pusat, yang disebut akar. Setiap cabang mewakili sebuah simpul, dan setiap simpul dapat memiliki anak-anak dan orang tua. Struktur hierarkis ini memungkinkan pengorganisasian dan pencarian data yang efisien.
Pemahaman Topologi Tree: Gambar Topologi Tree
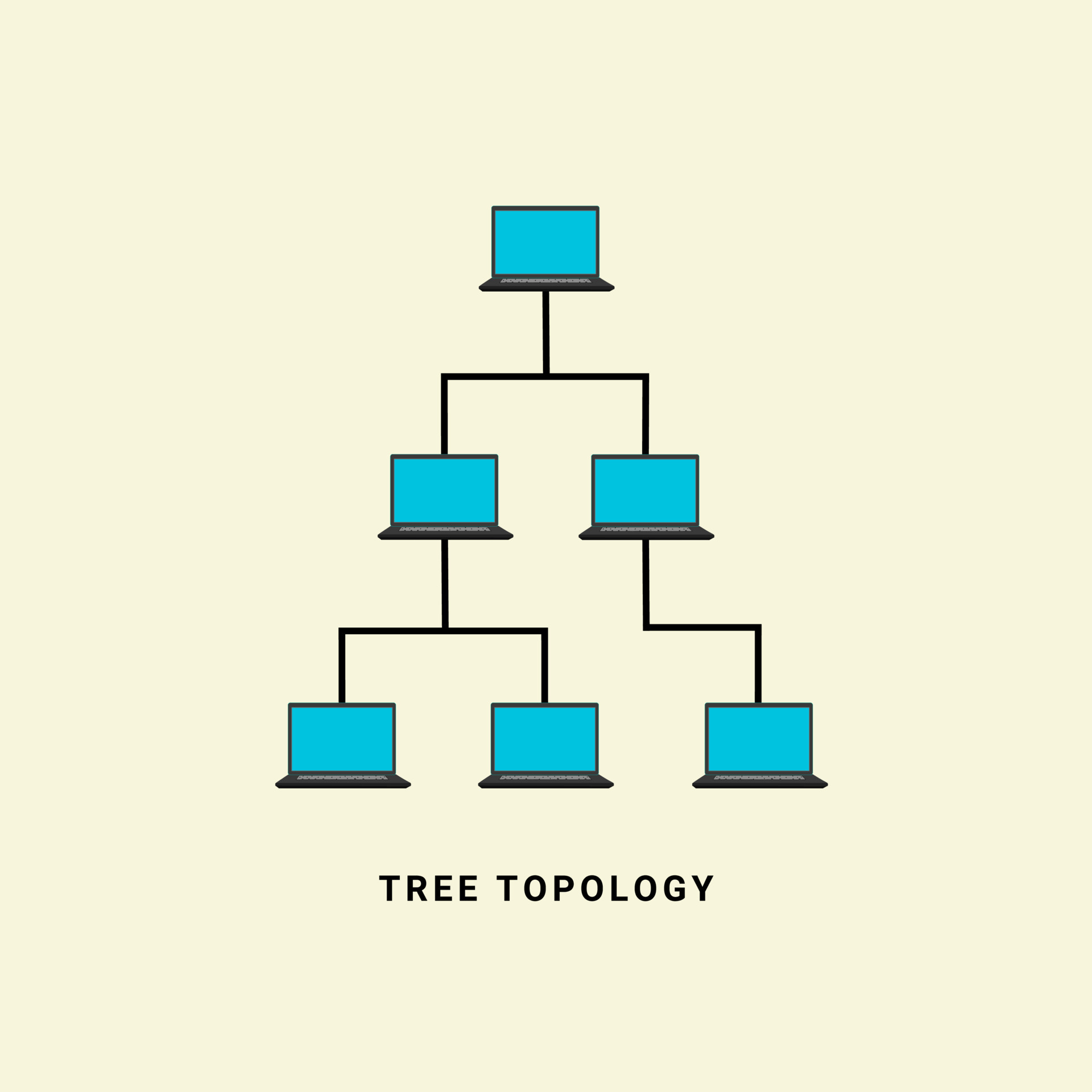
Topologi tree adalah struktur data hierarkis yang menghubungkan simpul-simpul dengan cara yang membentuk pohon. Setiap simpul memiliki satu simpul induk, kecuali simpul teratas yang disebut root. Simpul-simpul yang tidak memiliki anak disebut leaf.
Dalam topologi tree, simpul-simpul terhubung secara hierarkis, membentuk struktur seperti pohon. Nah, menariknya, kita bisa memanfaatkan pengetahuan tentang jaringan ini untuk mencari tahu password Wi-Fi yang sudah terhubung. Dengan mengikuti langkah-langkah cara melihat password wifi yang sudah terhubung , kita dapat mengakses kata sandi yang tersimpan di perangkat kita.
Setelah mengetahui password, kita bisa kembali ke topik topologi tree dan melanjutkan eksplorasi struktur jaringan yang lebih kompleks.
Struktur Tree
Struktur tree terdiri dari:
- Root:Simpul teratas yang tidak memiliki induk.
- Parent:Simpul yang memiliki satu atau lebih anak.
- Child:Simpul yang memiliki satu induk.
- Leaf:Simpul yang tidak memiliki anak.
Kegunaan Topologi Tree
Topologi tree memiliki berbagai kegunaan, di antaranya:
- Menyimpan data hierarkis, seperti struktur organisasi atau sistem file.
- Melakukan pencarian dan pengurutan yang efisien.
- Menunjukkan hubungan antar entitas, seperti dalam jaringan komputer.
Contoh Topologi Tree
Berikut adalah contoh topologi tree yang mewakili struktur organisasi:
CEO
/ \
Manager1 Manager2
/ / \
Employee1 Employee2 Employee3
Jenis Topologi Tree
Dalam topologi jaringan, topologi tree merupakan struktur hierarkis di mana setiap node terhubung ke node lain, membentuk sebuah jalur yang menghubungkan semua node.
Binary Tree
Binary tree adalah topologi tree di mana setiap node memiliki maksimal dua anak. Struktur ini sering digunakan dalam pencarian biner dan pohon biner.
Balanced Tree
Balanced tree adalah topologi tree di mana perbedaan tinggi antara subtree kiri dan kanan setiap node tidak lebih dari 1. Struktur ini memastikan operasi pencarian dan penyisipan yang efisien.
AVL Tree
AVL tree adalah jenis balanced tree yang menggunakan faktor keseimbangan untuk mempertahankan keseimbangan. Faktor keseimbangan adalah perbedaan tinggi antara subtree kiri dan kanan setiap node. AVL tree memastikan operasi pencarian dan penyisipan yang efisien, bahkan untuk data yang tidak berurutan.
Aplikasi Topologi Tree
Topologi tree banyak digunakan dalam berbagai aspek kehidupan, termasuk:
Struktur Data dan Algoritma
- Pohon pencarian biner (BST): Digunakan untuk menyimpan dan mengambil data secara efisien, menjaga urutan.
- Pohon heap: Digunakan untuk mengimplementasikan struktur data prioritas, mengakses elemen dengan prioritas tertinggi dengan cepat.
- Pohon trie: Digunakan untuk menyimpan data yang terkait dengan awalan dan sufiks, memungkinkan pencarian dan pengambilan yang efisien.
Komputasi
- Sistem file hierarkis: Mengatur file dan direktori dalam struktur tree, memudahkan navigasi dan pengambilan.
- Struktur direktori: Digunakan untuk mengatur file dan folder pada komputer, memungkinkan akses dan pengambilan yang terorganisir.
- Pohon parse: Digunakan dalam kompilasi dan interpretasi bahasa pemrograman, mewakili struktur sintaksis dari program.
Organisasi dan Pencarian Data
- Pohon XML: Digunakan untuk mewakili data terstruktur dalam format XML, memungkinkan pengambilan dan manipulasi data yang efisien.
- Pohon keputusan: Digunakan untuk pengambilan keputusan, mewakili urutan keputusan dan konsekuensinya.
- Pohon hierarki: Digunakan untuk merepresentasikan hubungan hierarkis, seperti dalam bagan organisasi atau pohon keluarga.
Algoritma pada Topologi Tree
Topologi tree merupakan struktur data hierarkis yang digunakan untuk merepresentasikan hubungan antar data. Algoritma pada topologi tree dirancang untuk memanipulasi dan mengelola struktur ini secara efisien.
Algoritma traversal digunakan untuk mengunjungi setiap node dalam tree. Ada tiga jenis traversal umum: preorder, inorder, dan postorder. Kompleksitas waktu untuk traversal adalah O(n), di mana n adalah jumlah node dalam tree.
Pencarian
Algoritma pencarian digunakan untuk menemukan node tertentu dalam tree. Algoritma umum untuk pencarian adalah depth-first search (DFS) dan breadth-first search (BFS). Kompleksitas waktu untuk DFS dan BFS adalah O(n), di mana n adalah jumlah node dalam tree.
Penyisipan
Algoritma penyisipan digunakan untuk menambahkan node baru ke tree. Kompleksitas waktu untuk penyisipan adalah O(log n), di mana n adalah jumlah node dalam tree.
Penghapusan
Algoritma penghapusan digunakan untuk menghapus node dari tree. Kompleksitas waktu untuk penghapusan adalah O(log n), di mana n adalah jumlah node dalam tree.
Implementasi Topologi Tree
Topologi tree dapat diimplementasikan dalam berbagai bahasa pemrograman. Umumnya, terdapat dua struktur data utama yang digunakan:
- Node: Menyimpan data dan referensi ke node anak.
- Tree: Menyatukan node-node dan menyediakan metode untuk mengakses dan memanipulasi struktur.
Operasi Dasar
Beberapa operasi dasar yang dapat dilakukan pada tree meliputi:
- Insert: Menambahkan node baru ke tree.
- Delete: Menghapus node dari tree.
- Search: Mencari node dengan nilai tertentu.
- Traversal: Mengunjungi semua node dalam tree dengan urutan tertentu.
Pertimbangan Implementasi
Saat mengimplementasikan topologi tree, ada beberapa pertimbangan penting:
- Alokasi Memori: Setiap node dalam tree membutuhkan memori untuk menyimpan data dan referensi. Alokasi memori yang efisien sangat penting untuk tree besar.
- Efisiensi: Operasi seperti pencarian dan traversal harus efisien. Pemilihan struktur data yang tepat dan algoritma traversal yang optimal dapat meningkatkan efisiensi.
Contoh Kode, Gambar topologi tree
Berikut adalah contoh kode implementasi tree sederhana dalam Python:“`pythonclass Node: def __init__(self, data): self.data = data self.children = []class Tree: def __init__(self): self.root
= None def insert(self, data): new_node = Node(data) if self.root is None: self.root
= new_node else: self._insert(new_node, self.root) def _insert(self, new_node, current_node): if new_node.data < current_node.data: if len(current_node.children) == 0: current_node.children.append(new_node) else: self._insert(new_node, current_node.children[0]) else: if len(current_node.children) == 1: current_node.children.append(new_node) else: self._insert(new_node, current_node.children[1]) def search(self, data): if self.root is None: return None else: return self._search(data, self.root) def _search(self, data, current_node): if data == current_node.data: return current_node elif data < current_node.data: if len(current_node.children) == 0: return None else: return self._search(data, current_node.children[0]) else: if len(current_node.children) == 1: return None else: return self._search(data, current_node.children[1]) ```
Simpulan Akhir
Gambar topologi pohon memberikan wawasan yang mendalam tentang struktur data pohon yang kuat ini.
Dengan memahami konsep dan jenis pohon topologi yang berbeda, kita dapat memanfaatkannya secara efektif untuk berbagai aplikasi, termasuk pencarian, pengurutan, dan penyimpanan data.
